Mathematics is the main branch of science that deals with space, change, quality, and structure. There are further sub-branches of mathematics such as calculus, algebra, and geometry. The term calculus deals with the study of continuous change.
Algebra is the study of generalizations of arithmetic operations while geometry is the study of shapes. In this post, we are going to explain the term calculus along with its types, formulas, and solved examples.
What is calculus?
Calculus is one of the main branches of mathematics that deals with continuous change or rate of change. It is the calculation of instantaneous rates of change and the summation of an infinite number of small factors in order to determine some whole.
It covers the basic topics of mathematics such as the differential, integral, limits, Taylor series, Maclaurin series, trigonometry, etc. Calculus is a branch of mathematics that is developed by Gottfried Leibniz and Isaac Newton to study the rate of change of functions.
It is generally used to obtain optimal solutions in mathematical models and helps learn the changes among the different values of the function. Calculus is divided into the following categories.
- Differential Calculus
- Integral Calculus
- Limit calculus
What is a function in calculus?
The relationship between two variables such as the independent variable and the dependent variable is said to be a function in calculus. Such as y = f(x) is said to be “y” is the function of “x” in which y is a dependent variable and “x” is the independent variable. And is said to be y depending on x.
The functions could be linear, polynomial, exponential, logarithmic, trigonometric, hyperbolic, etc.
Branches of Calculus
There are three well-known branches of calculus.
- Differential Calculus
- Integral Calculus
- Limit calculus
Let us explain the branches of calculus briefly.
Differential Calculus
The first branch of calculus is differential calculus which is helpful for determining the rate of change of a function (y = f(x)) with respect to independent variables. The differential calculus is essential for evaluating the minimum and maximum values of the function in case to evaluate the optimal solution.
The limit of the quotient and changes in the dependent and independent variables occur with the help of this branch of calculus. The differential calculus is denoted by d/dx [y = f(x)] or f’(x). The independent variable of the function could be x, y, z, u, v, w, etc.
Such as the derivative of “y” w.r.t “x” is written as dy/dx
The derivative of “y” w.r.t “z” is written as dy/dz
The derivative of “f(u)” w.r.t “u” is written as d[f(u)]/du
Types of differential calculus
Differential calculus is further divided into different categories to differentiate various kinds of functions.
- Explicit derivative
- Implicit differentiation
- Partial differentiation
- Directional derivative
These types of differential calculus are helpful for differentiating the single variable function, a derivative of an equation, the differential of the multivariable function, and the direction of the differential function.
All types of differential calculus are used in different scenarios for various purposes. The notation and expression for the types of differential calculus are given below.
| Types | Function | Notation |
| Explicit differentiation | f(x), f(y), f(z), etc. | d/dx [f(x)], d/dy [f(y)], etc. |
| Implicit differentiation | f(x, y) = g(x, y) | dy/dx |
| Partial derivative | f(x, y, z) | ∂/∂x, ∂/∂y, and ∂/∂z |
| Directional derivative | ∇u (f(x, y) = ∇ f(x, y) * u /|u| | f’u(x, y), v. ∇ f(x, y), ∇u (x, y) |
Integral Calculus
The second well-known branch of calculus is an integration that deals with the integral and its properties. It is essential for finding the area under the curve with the help of boundary values of the given function.
It is also essential for evaluating the original function from the differential function. Such as if a function f’(x) (a derivative of a function) is given then the integral will calculate f(x) (original function).
The reverse process of differentiation is said to be integration. For instance, you can understand the term integration as if the differential calculus divides apart into many small parts then the integral will collect all the small parts to complete the original part.
Types of integral calculus
Integral calculus is further divided into two types.
- Definite integral
- Indefinite integral
The definite integral is helpful for finding the area under the curve with the help of boundary values such as the upper limit and the lower limit. While the indefinite integral is used to define the original function from the differential function. There are no boundary points involved in the indefinite integral.
| Definite integral formula | ∫ab f(x) dx = [F(x)] ab = F(b) – F(a) |
| Indefinite integral formula | ∫ f(x) dx = F(x) + C |
Limit Calculus
Limit calculus is a well-known branch of calculus that is helpful for defining the other types of calculus such as integral, differential, Taylor series, continuity, etc. This branch of calculus is helpful in evaluating the closeness of the values to the function or approaching term to the function or to the specific point.
The limit is defined as “the limit of a function f of “x” as x approaches “a” equals to L”. Mathematically it can be written as:
limx→a [f(x)] = L
Types of Limit calculus
There are three basic types of limit calculus used to evaluate the problems of the limits.
- Left-hand limit
- Right-hand limit
- Two-sided limit
When the values of the function approach the specific point or limits from the left is said to be the left-hand limit. When the values of the function approach the specific point or limits from the right are said to be the right-hand limit.
When the left-hand limit and right-hand limit hold for a function then it is said to be the two-sided limit.
| Types | Mathematical expression |
| Left-hand limit | limx→a– [f(x)] = L |
| Right-hand limit | limx→a+ [f(x)] = L |
| Two-sided limit | limx→a [f(x)] = L |
Formulas of calculus
Here are some well-known formulas of calculus.
| Formulas of integral | Formulas of differential | Formulas of limits |
| ∫ xn dx = xn + 1/(n + 1) + C | d/dx [xn] = n * xn – 1d/dx[x] | limx→0 [(sin(x))/x] = 1 |
| ∫ 1 dx = x + C | d/dx [C] = 0 | limx→0 [(tan(x))/x] = 1 |
| ∫ ex dx = ex + C | d/dx [ex] = ex | limx→0 (ex – 1)/x = 1 |
| ∫ sec(x) tan(x) dx = sec(x)+C | d/dx [ax] = ax * log(a) | limx→0 (1 + (1/x))x = e |
| ∫ ax dx = (ax/log a) + C | d/dx [log x] = 1/x | limx→0 (1 + x)1/x = e |
| ∫ cosec2(x) dx = -cot(x) + C | d/dx [cosec x] = -cosec(x) * cot(x) | limx→0 (1 + (a/x))x = ea |
| ∫ sec2(x) dx = tan(x) + C | d/dx [sec x] = sec(x) * tan(x) | limx→0 (ax – 1)/x = logea |
How to evaluate calculus problems?
The problems of calculus can be solved with the help of formulas and rules of calculus.
Example 1: For Derivative Calculus
Example 1
Find the differential of f(u) = 6u3 – 4u2 + 2u2 + 5u + sin(u) – 3u4 with respect to “u”.
Solution
Step 1: First of all, take the given algebraic expression and apply the notation of differential to it.
d/du [f(u)] = d/du [6u3 – 4u2 + 2u2 + 5u + sin(u) – 3u4]
Step 2: Use the sum and difference laws of differential calculus and apply the notation of differential to each term of the function.
d/du [6u3 – 4u2 + 2u2 + 5u + sin(u) – 3u4] = d/du [6u3] – d/du [4u2] + d/du [2u2] + d/du [5u] + d/du [sin(u)] – d/du [3u4]
Step 3: Now use the constant of a function law to the above expression.
d/du [6u3 – 4u2 + 2u2 + 5u + sin(u) – 3u4] = 6d/du [u3] – 4d/du [u2] + 2d/du [u2] + 5d/du [u] + d/du [sin(u)] – 3d/du [u4]
Step 4: Now take the above expression with the help of the power and trigonometric laws of differential calculus.
d/du [6u3 – 4u2 + 2u2 + 5u + sin(u) – 3u4] = 6 [3u3-1] – 4 [2u2-1] + 2 [2u2-1] + 5 [u1-1] + [cos(u)] – 3 [4u4-1]
d/du [6u3 – 4u2 + 2u2 + 5u + sin(u) – 3u4] = 6 [3u2] – 4 [2u1] + 2 [2u1] + 5 [u0] + [cos(u)] – 3 [4u3]
= 6 [3u2] – 4 [2u] + 2 [2u] + 5 [1] + [cos(u)] – 3 [4u3]
= 18u2 – 8u + 4u + 5 + cos(u) – 12u3
= 18u2 – 4u + 5 + cos(u) – 12u3
Example 2: For Integral Calculus
Find the integral of f(v) = 5v2 – 4v3 + 6v6 + 2v5 + 5
Solution
Step 1: First of all, take the given algebraic expression and apply the notation of integration to it.
ʃ f(v) dv = ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv
Step 2: Use the sum and difference laws of integral calculus and apply the notation of integral to each term of the function.
ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv = ʃ [5v2] dv – ʃ [4v3] dv + ʃ [6v6] dv + ʃ [2v5] dv + ʃ [5] dv
Step 3: Now use the constant of a function law to the above expression.
ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv = 5ʃ [v2] dv – 4ʃ [v3] dv + 6ʃ [v6] dv + 2ʃ [v5] dv + ʃ [5] dv
Step 4: Now find the integral of the above expression.
ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv = 5 [v2+1 / 2 + 1] – 4 [v3+1 / 3 + 1] + 6 [v6+1 / 6 + 1] + 2 [v5+1 / 5 + 1] + [v] + C
ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv = 5 [v3 / 3] – 4 [v4 / 4] + 6 [v7 / 7] + 2 [v6 / 6] + [v] + C
ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv = 5v3/3 – 4v4/4 + 6v7/7 + 2v6/6 + v + C
ʃ [5v2 – 4v3 + 6v6 + 2v5 + 5] dv = 5v3/3 – v4/ + 6v7/7 + v6/3 + v + C
Example 3: For Limit Calculus
Calculate the limit of f(w) = 2w3 + 6w2 – 5w * 6w + 4 if the specific value is 5.
Solution
Step 1: First of all, take the given algebraic expression and apply the notation of limit to it.
Limw→a [f(w)] = limw→5 [2w3 + 6w2 – 5w * 6w + 4]
Step 2: Use the sum and difference laws of limit calculus and apply the notation of limit to each term of the function.
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = limw→5 [2w3] + limw→5 [6w2] – limw→5 [5w] * limw→5 [6w] + limw→5 [4]
Step 3: Now use the constant of a function law to the above expression.
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = 2limw→5 [w3] + 6limw→5 [w2] – 5limw→5 [w] * 6limw→5 [w] + limw→5 [4]
Step 4: Now place the articular value z = 2 to the above expression to evaluate the limit.
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = 2 [53] + 6 [52] – 5 [5] * 6 [5] + [4]
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = 2 [5 * 5 * 5] + 6 [5 * 5] – 5 [5] * 6 [5] + [4]
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = 2 [125] + 6 [25] – 5 [5] * 6 [5] + [4]
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = 250 + 150 – 25 * 30 + 4
limw→5 [2w3 + 6w2 – 5w * 6w + 4] = -346
Alternatively
The above problems of calculus can be solved easily with the help of online calculators. Let’s solve the above 3 examples using calculators.
Example 1
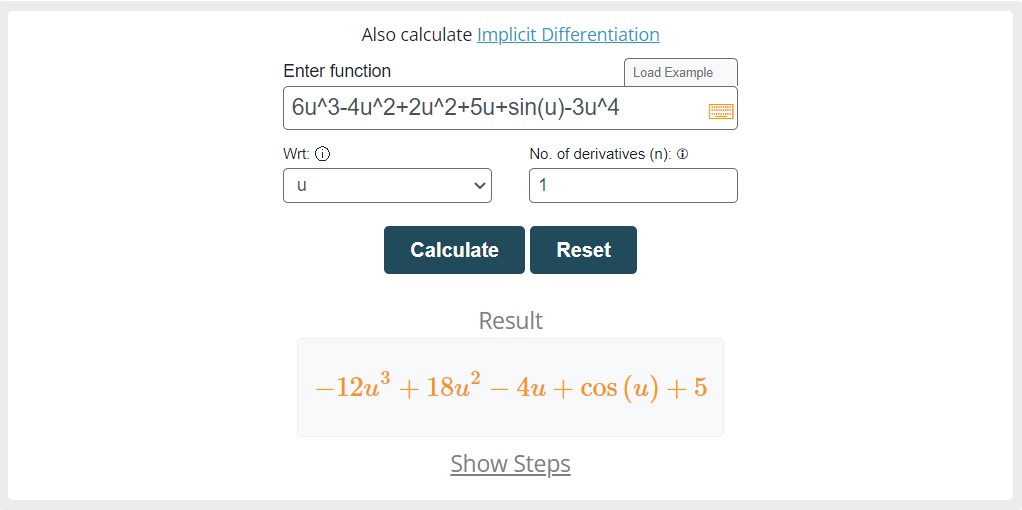
Solved through derivative calculator by meracalculator.com
Example 2:
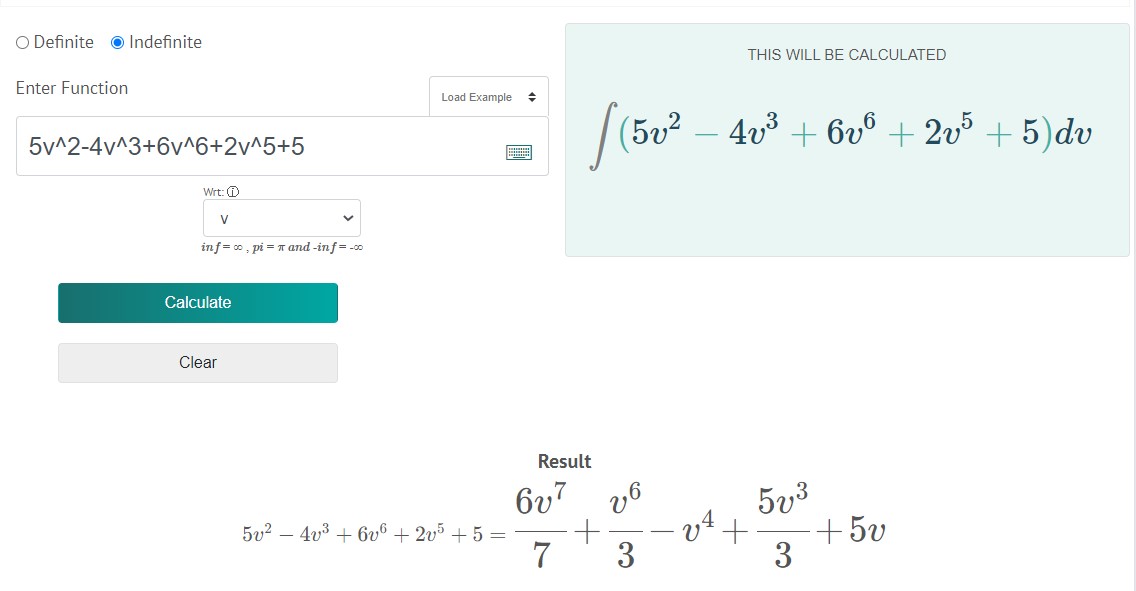
Solved through antiderivativecalculator.net
Example 3:
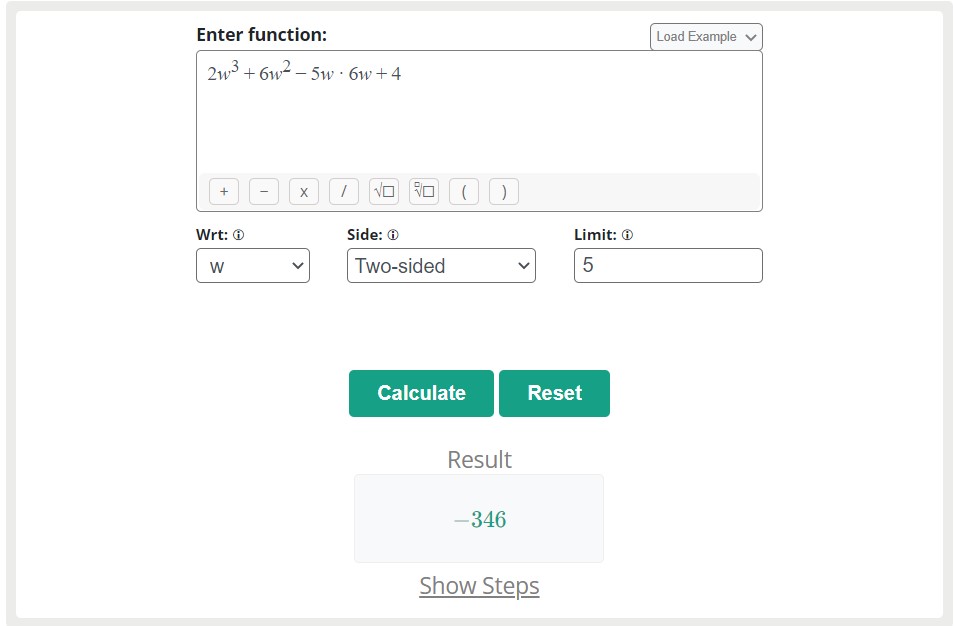
Solved through limit calculator by allmath.com
Final Words
Now you can take all the basics of calculus from one platform. We have covered the definition, types, formulas, and solved examples of calculus for understanding this topic accurately. The concept of limit, integral, and differential are also discussed.


























